Cost per hire is the amount it costs you to make a hire. As it’s difficult and time-consuming to work this out for every single job, normally it is an average cost over a period of time (a month or year).
The formula for calculating cost per hire is:

Internal costs
Basically, you want to include how much it costs to run your internal talent acquisition team. This can include:
- Salaries, including any employer taxes
- Benefits, such as pension and health insurance
- Equipment and stationary - laptops, phones, printing, etc.
- IT support and basic software (email, Office, G suite, etc.)Any training or staff development costs
- Travel
- Office costs
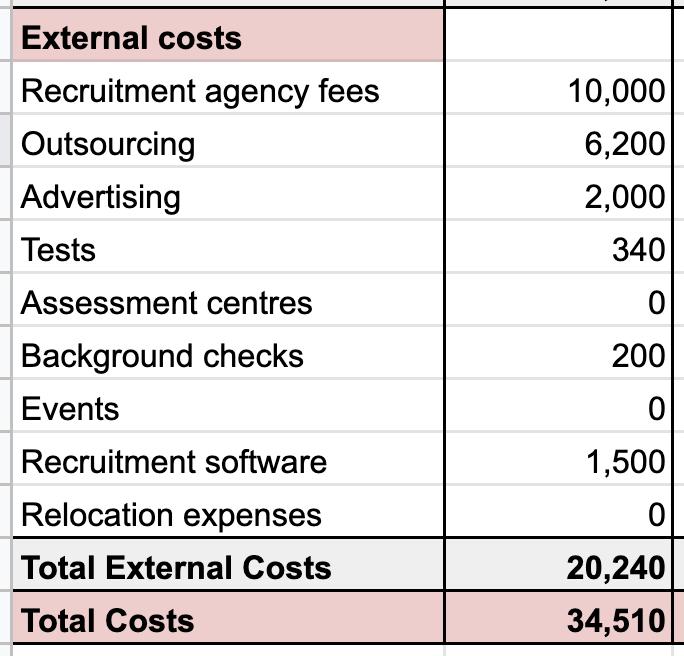
External costs
External costs are amounts spent on talent acquisition with other companies. Some of the common types of external costs are:
- Recruitment agency fees
- Outsourcing - Recruitment Process Outsourcing and external contractors
- Advertising - job boards, Facebook, LinkedIn, etc.
- Tests - such as aptitude, psychometric, work sample tests, assessment centres
- Background checks
- Events
- Recruitment software - e.g. Applicant Tracking System, sourcing software
- Relocation expenses - the cost of moving new staff, including visas and legal fees
Number of hires
With the total number of hires, you’re trying to work out how many people joined the company during the month or year.
Generally, this will include all full-time and part-time staff. And exclude consultants, people joining due to a merger and employees that are paid by a third party.
But there are a few areas that are not so clear cut:
- Temp staff promoted to a permanent position (more likely include)
- Internal transfers (more likely exclude)
- Contractors - may depend on how much time and effort your company (recruiters and hiring manager) spend on these positions.
For these roles, you’ll need to make a call whether you include them or not. As long as you’re consistent you’ll be able to see trends in your data.
Just be careful when comparing your results to other companies. If they treat these hires differently, you may not be making a fair comparison.
Why you should measure cost per hire
Understanding how much you’re spending to hire people can help you improve your hiring process.
For example, you may find that you’re spending less when your in-house team hires someone than when you use an agency or RPO (Recruitment Process Outsourcing) firm. You could then use this to justify investing in your in-house team.
Similarly, you might know that there is a tool that could save your team’s time. If the time saved meant that you didn’t use as many agencies, you could show this as a cost saving. Or, if it meant you could hire more people with your current team, you’ll see a saving in the overall cost per hire.
But while costs are important, you need to look at other areas of your hiring process too.
If you were to focus only on lowering costs, a realistic side-effect is a drop in the quality of the people you hire. Or work not getting done because it’s taking you longer to hire the people needed to do it. Both of these things can result in lost revenue and may end up costing the company more than what you saved in hiring costs.
How to calculate cost per hire
As every company tracks its costs, calculating your cost per hire isn’t too difficult. In this guide, we’ll look at how to set up a spreadsheet to capture the data you need and complete the calculation each month.
To help, I’ve created a spreadsheet template for you, which will calculate your cost per hire and chart it for the year.
Step 1 - Get you cost data
The first thing you’ll need is a cost report. What is available, and in what format, will depend on your company. But every company should have monthly cost reports.
To start with, use the cost report for the previous month. If possible, try and get it for the talent acquisition team only (or however your in-house recruitment team is named).
If your company doesn’t have a report for the talent acquisition team only, get the next best report available, such as for HR. We’ll cover how to split out the costs you need below.
Step 2 - Record your internal costs
For internal costs, we want to capture all the costs of your talent acquisition (in-house recruitment) team. The types of costs to include are listed above.
👉 The goal is to make updating the spreadsheet as easy as possible. So you may want to add or remove rows and update the names in the spreadsheet to match those in your cost report.
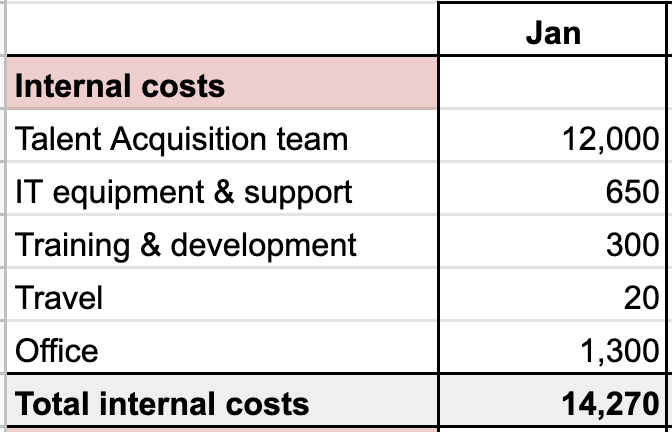
If your cost report covers more people than the talent acquisition team, such as all of HR, you’ll need to make an adjustment to remove the costs of people not in talent acquisition.
An easy way to do this is to multiply the total costs you have by a percentage, then add them to the spreadsheet. This won’t be completely accurate but may be a good approximation.
For example, say you could only get a cost report for HR. In HR, you have a total of 8 people and 3 of them are in the talent acquisition team. In this case, 3 ÷ 8, or 37.5% of the costs related to the talent acquisition team. So you add 37.5% of each of the cost categories to your spreadsheet.
Step 3 - Add your external costs
Next, add your external costs. Again, update the rows to match your report so it’s easy to fill out in the future.
If your report is for a larger team, such as HR, you may still be able to find the recruitment related to external costs. If you can you won’t need to split the costs.
One area to be careful of is software costs. Your report may have one amount that includes software that we want to split between internal and external. If this is the case, add the recruitment software to the external costs first. Then the internal costs will be the total software costs less the external costs.
Step 4 - Add your hires
The final step is to add the number of people you hired in the month. You can use the definition above to work out which types of hire to include and exclude.

👉Then, if you’re using our spreadsheet it’ll calculate the cost per hire for you.

👉Additionally, it’ll create a chart so you can follow how your monthly cost per hire moves throughout the year.
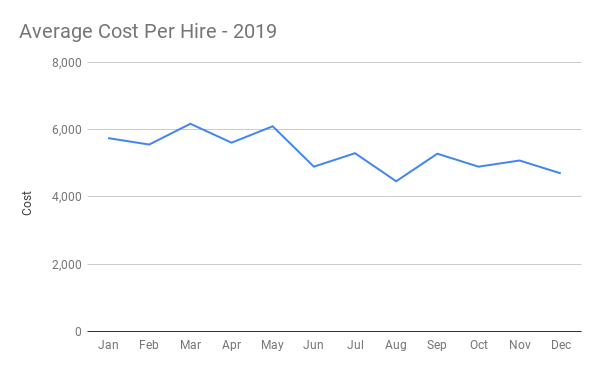
What’s next?
All you need to do now is repeat the four steps each month.
You’ll probably find that many of the costs don’t change each month - so it should get easier and quicker to complete.
You can also go back and complete the previous months so you can see if there are any trends. Like in the example chart above, you can see the average cost per hire varies a bit each month, but the overall trend is down.
Got a question or request?
I’d love to hear from you and help out - you can reach me here.




